Вводная часть

Состав исследовательской команды

Студенты группы НФИбд-01/02-22:

• Абакумова Олеся Максимовна
• Астраханцева Анастасия Александровна
• Ганина Таисия Сергеевна
• Ибатулина Дарья Эдуардовна

Постановка проблемы

Традиционные методы моделирования газовых потоков и жидкостей требуют значительных вычислительных ресурсов, что затрудняет их применение для сложных задач. В связи с этим возникает необходимость разработки более эффективных и простых в реализации моделей, способных адекватно описывать поведение газов на микроскопическом уровне. Модели решеточных газов (LGA) и решеточного уравнения Больцмана (LBE) представляют собой такой подход, позволяющий упростить вычисления, сохраняя при этом физическую достоверность.

Актуальность

Методы LGA и LBE важны в гидродинамике и биофизике благодаря эффективности. Модель HPP - основа для более сложных моделей. Важно реализовать и протестировать HPP для проверки алгоритмов.

Цель

Разработать и проанализировать модель на основе решеточного уравнения Больцмана для описания течений газа.

Задачи третьего этапа проекта

1. Реализовать и описать программный алгоритм решения задачи на языке Julia.

Основная часть

Модель HPP (Hardy–Pomeau–Pazzis)

Модель HPP (Hardy-Pomeau-Pazzis) — это базовая модель решеточных газов (LGA), используемая для моделирования гидродинамических явлений на микроскопическом уровне. Она представляет собой дискретную систему, где пространство и время дискретизованы, а частицы двигаются по узлам квадратной решетки.

Основные характеристики

1. Решетка: Двумерная квадратная
2. Частицы: Единичной массы, 4 направления
3. Скорость: Δx/Δt = 1
4. Принцип исключения: ≤1 частица/направление
5. Эволюция: Распространение → Столкновения
6. Столкновения: Сохранение импульса, 90° поворот
7. Кодирование: 4-битный формат (1 бит/направление)

Математическое описание:

Обозначим возможные направления скорости как $d_1, d_2, d_3, d_4$$. Тогда:

• $d_1 = 0001_2 = 1$

• $d_2 = 0010_2 = 2$

• $d_3 = 0100_2 = 4$

• $d_4 = 1000_2 = 8$

Основные операции для работы с состояниями узлов

1. Добавление частицы: добавление к состоянию $S$ частицы с направлением скорости $d_k$: $$ S \text{ OR } d_k \rightarrow S $$

2. Проверка наличия частицы: проверка, есть ли в состоянии $S$ частица с направлением скорости $d_k$: $$ \text{if } (S \text{ AND } d_k) \neq 0 $$ Если результат не равен 0, то частица с направлением $d_k$ присутствует в узле.

Недостатки модели HPP

1. Отсутствие симметрии

2. Нефизичное поведение

Описание задания

Реализуйте модель HPP. Задайте периодические граничные условия. Это просто сделать, добавив по одному ряду узлов с каждой стороны области (фиктивные узлы). Перед шагом распространения необходимо скопировать значения левого ряда физических узлов в правый фиктивный ряд. Тогда частицы, вылетая из левой границы области налево, появятся на ее правой границе. С другими границами поступают также. Вначале возьмите одну единственную частицу и проверьте правильность всех граничных условий. Затем убедитесь, что для двух частиц их столкновения “почти лоб в лоб” и под прямым углом происходят верно. Для любого числа частиц должны сохраняться их полное число и полный импульс.

Описание программного кода

Код для модели HPP мы реализовали на языке Julia.

Применение периодических граничных условий

function apply_periodic_boundaries!(grid)
    for d in 1:4
        grid[1, 2:Ny+1, d] .= grid[Nx+1, 2:Ny+1, d]     
        # левая фиктивная = правая физическая
        grid[Nx+2, 2:Ny+1, d] .= grid[2, 2:Ny+1, d]     
        # правая фиктивная = левая физическая
        grid[2:Nx+1, 1, d] .= grid[2:Nx+1, Ny+1, d]     
        # нижняя фиктивная = верхняя физическая
        grid[2:Nx+1, Ny+2, d] .= grid[2:Nx+1, 2, d]     
        # верхняя фиктивная = нижняя физическая
    end
end

Обработка столкновений частиц

function collide!(grid)
    for x in 2:Nx+1, y in 2:Ny+1
        right, up, left, down = grid[x,y,1], 
                                grid[x,y,2], 
                                grid[x,y,3], 
                                grid[x,y,4]
        if right && left && !up && !down
            grid[x,y,1] = false
            grid[x,y,3] = false
            grid[x,y,2] = true
            grid[x,y,4] = true
        elseif up && down && !right && !left
            grid[x,y,2] = false
            grid[x,y,4] = false
            grid[x,y,1] = true
            grid[x,y,3] = true
        end
    end
end

Распространение частиц

function propagate!(grid)
    new_grid = zeros(Bool, size(grid))
    for x in 2:Nx+1, y in 2:Ny+1, d in 1:4
        if grid[x, y, d]
            nx, ny = x + dx[d], y + dy[d]
            new_grid[nx, ny, d] = true
        end
    end
    return new_grid
end

Первый тест

• test_single_particle() - одна частица в центре движется вправо, проверяется распространение и периодичность.

Первый тест, код

# Тест 1: Одна частица
function test_single_particle()
    grid = create_grid()
    add_particle!(grid, Nx÷2, Ny÷2, 1)  # Частица в центре, движется вправо
    
    anim = @animate for step in 1:20
        apply_periodic_boundaries!(grid)
        collide!(grid)
        p = plot_grid(grid, step)
        grid = propagate!(grid)
        n = count_particles(grid)
        px, py = calculate_momentum(grid)
        annotate!(p, 0.5, Ny+1.2, text("Particles: $n", :left))
        annotate!(p, 0.5, Ny+0.8, text("Momentum: ($px, $py)", :left))
        
        p
    end
    
    gif(anim, "hpp_single_particle.gif", fps=2)
end

Запуск теста №1. Одна частица в центре, движется вправо. Шаг №1

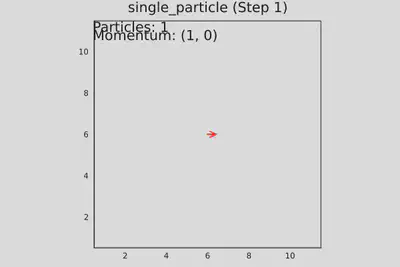
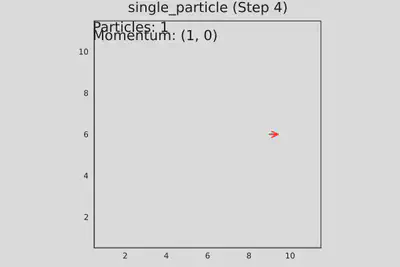
Запуск теста №1. Одна частица в центре, движется вправо. Шаг №2

Запуск теста №1. Одна частица в центре, движется вправо. Шаг №4

Второй тест

• test_head_on_collision() - две частицы движутся навстречу, проверяется лобовое столкновение.

Второй тест, код

# Тест 2: Две частицы (лобовое столкновение)
function test_head_on_collision()
    grid = create_grid()
    add_particle!(grid, 4, 5, 1)  # →
    add_particle!(grid, 6, 5, 3)  # ←
    
    anim = @animate for step in 1:10
        apply_periodic_boundaries!(grid)
        collide!(grid)
        p = plot_grid(grid, step)
        grid = propagate!(grid)
        n = count_particles(grid)
        px, py = calculate_momentum(grid)
        annotate!(p, 0.5, Ny+1.2, text("Particles: $n", :left))
        annotate!(p, 0.5, Ny+0.8, text("Momentum: ($px, $py)", :left))
        
        p
    end
    
    gif(anim, "hpp_head_on.gif", fps=1)
end

Запуск теста №2. Две частицы движутся навстречу, лобовое столкновение. Шаг №1

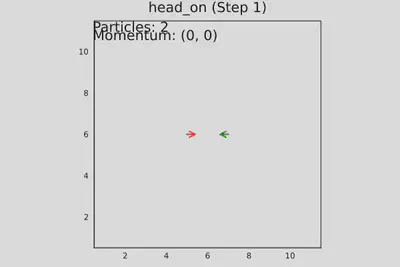
Запуск теста №2. Две частицы движутся навстречу, лобовое столкновение. Шаг №2

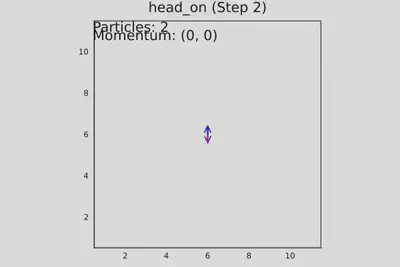
Запуск теста №2. Две частицы движутся навстречу, лобовое столкновение. Шаг №4

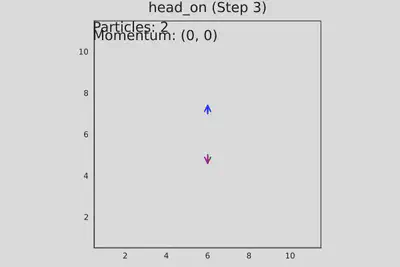
Третий тест

• test_right_angle_collision() - четыре частицы движутся навстречу под прямым углом, проверяется корректность столкновений.

Третий тест, код

# Тест 3: Четыре частицы (столкновение под прямым углом)
function test_right_angle_collision()
    grid = create_grid()
    add_particle!(grid, 5, 4, 2)  # ↑
    add_particle!(grid, 5, 6, 4)  # ↓
    add_particle!(grid, 4, 5, 1)  # →
    add_particle!(grid, 6, 5, 3)  # ←
    anim = @animate for step in 1:10
        apply_periodic_boundaries!(grid)
        collide!(grid)
        p = plot_grid(grid, step)
        grid = propagate!(grid)
        n = count_particles(grid)
        px, py = calculate_momentum(grid)
        annotate!(p, 0.5, Ny+1.2, text("Particles: $n", :left))
        annotate!(p, 0.5, Ny+0.8, text("Momentum: ($px, $py)", :left))
        p
    end
    gif(anim, "hpp_right_angle.gif", fps=1)
end

Запуск теста №3. Четыре частицы движутся навстречу под прямым углом. Шаг №1

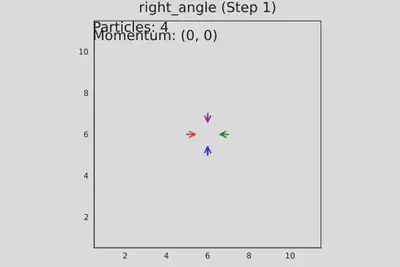
Запуск теста №3. Четыре частицы движутся навстречу под прямым углом. Шаг №2

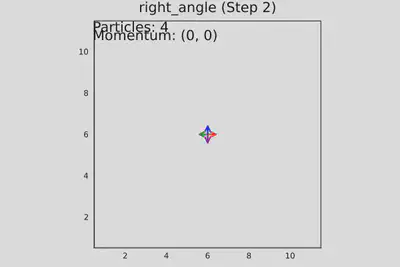
Запуск теста №3. Четыре частицы движутся навстречу под прямым углом. Шаг №3

Общая информация про тесты

В каждом тесте:

• Создаётся сетка.

• Добавляются частицы.

• В цикле на каждом шаге применяются граничные условия, столкновения, визуализация и распространение.

• Считается число частиц и импульс.

• Создаётся анимация и сохраняется в GIF.

Заключительная часть

Заключение

Модели решеточных газов $(LGA)$ и решеточное уравнение Больцмана $(LBE)$ представляют собой эффективные инструменты для моделирования газовых потоков. В данной части проекта мы рассмотрели простую базовую модель $HPP$.

Реализовали двумерную модель решеточного газа HPP с четырьмя направлениями движения, периодическими граничными условиями, обработкой столкновений и визуализацией. Тесты демонстрируют корректность работы модели и сохранение физических величин (число частиц и импульс).

Выводы

Во время выполнения третьего этапа группового проекта мы описали и реализовали модель HPP - базовую модель решеточных газов (LGA), которая может быть использована для моделирования решеточного уравнения Больцмана.

Список литературы

1. Медведев Д.А. и др. Моделирование физических процессов и явлений на ПК: Учеб. пособие. // Новосибирск: Новосиб. гос. ун-т, 2010. 101 с.

2. Succi, Sauro. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. Oxford University Press, 2001.