Введение

Цель проекта

Разработать и проанализировать модель на основе решеточного уравнения Больцмана для описания течений газа.

Задачи третьего этапа проекта

1. Реализовать и описать программный алгоритм решения задачи.

Актуальность

Моделирование газовых потоков и жидкостей традиционными методами требует значительных вычислительных ресурсов. В связи с этим, методы решеточных газов (LGA) и решеточного уравнения Больцмана (LBE) становятся все более актуальными. Они позволяют упростить вычисления, сохраняя при этом физическую достоверность, и находят применение в различных областях, от гидродинамики до биофизики. В данном докладе мы рассмотрим основные алгоритмы и модели, используемые для решения задач с применением LGA и LBE.

Основная часть

Модель HPP (Hardy–Pomeau–Pazzis)

Модель HPP (Hardy-Pomeau-Pazzis) — это базовая модель решеточных газов (LGA), используемая для моделирования гидродинамических явлений на микроскопическом уровне. Она представляет собой дискретную систему, где пространство и время дискретизованы, а частицы двигаются по узлам квадратной решетки.

Основные характеристики модели HPP:

1. Решетка: используется двумерная квадратная решетка, где узлы расположены на одинаковом расстоянии друг от друга.

2. Частицы: в каждом узле решетки могут находиться частицы единичной массы. Каждая частица может двигаться в одном из четырех направлений: вверх, вниз, вправо или влево.

3. Скорость: все частицы имеют одинаковую скорость, направленную к соседнему узлу. Расстояние между узлами ($\Delta x$) и шаг времени ($\Delta t$) выбираются так, чтобы частица могла переместиться в соседний узел за один временной шаг.

4. Принцип исключения: в каждом узле может находиться не более одной частицы, движущейся в заданном направлении.

5. Этапы эволюции:

   • Распространение (Streaming): частицы перемещаются в соседние узлы в соответствии со своими скоростями. За один шаг времени частица переходит в соседний узел в направлении своего движения.
   • Столкновения (Collision): в узлах происходят столкновения частиц, при которых сохраняются количество частиц и полный импульс.

6. Правила столкновений: столкновения происходят таким образом, чтобы выполнялись законы сохранения. В модели HPP нетривиальные столкновения происходят, когда две частицы движутся навстречу друг другу (почти “лоб в лоб”). После столкновения частицы меняют направления движения на 90 градусов. Во всех остальных случаях столкновения считаются несущественными, и частицы продолжают двигаться в прежних направлениях.

7. Кодирование состояний: состояние каждого узла решетки кодируется битами. Поскольку имеется четыре возможных направления движения, для кодирования состояния узла требуется четыре бита. Каждый бит соответствует одному из направлений: 0 — нет частицы, 1 — есть частица, движущаяся в этом направлении. Например, если частицы движутся вправо и вверх, состояние узла кодируется как 0101 в двоичном формате [@medvedev2010, @chaschin2021]

Математическое описание:

Обозначим возможные направления скорости как $d_1, d_2, d_3, d_4$$. Тогда:

• $d_1 = 0001_2 = 1$

• $d_2 = 0010_2 = 2$

• $d_3 = 0100_2 = 4$

• $d_4 = 1000_2 = 8$

Основные операции для работы с состояниями узлов:

1. Добавление частицы: добавление к состоянию $S$ частицы с направлением скорости $d_k$: $$ S \text{ OR } d_k \rightarrow S $$

2. Проверка наличия частицы: проверка, есть ли в состоянии $S$ частица с направлением скорости $d_k$: $$ \text{if } (S \text{ AND } d_k) \neq 0 $$ Если результат не равен 0, то частица с направлением $d_k$ присутствует в узле.

Недостатки модели HPP:

1. Отсутствие симметрии: квадратная решетка с четырьмя направлениями скорости недостаточно симметрична, что приводит к анизотропии в макроскопических свойствах.

2. Нефизичное поведение: модель HPP неточно описывает гидродинамические свойства жидкостей и газов.

Для устранения этих недостатков были разработаны более совершенные модели, такие как FHP (Frisch-Hasslacher-Pomeau) на треугольных решетках и модели с добавлением покоящихся частиц.

Описание задания

Реализуйте модель HPP. Задайте периодические граничные условия. Это просто сделать, добавив по одному ряду узлов с каждой стороны области (фиктивные узлы). Перед шагом распространения необходимо скопировать значения левого ряда физических узлов в правый фиктивный ряд. Тогда частицы, вылетая из левой границы области налево, появятся на ее правой границе. С другими границами поступают также. Вначале возьмите одну единственную частицу и проверьте правильность всех граничных условий. Затем убедитесь, что для двух частиц их столкновения “почти лоб в лоб” и под прямым углом происходят верно. Для любого числа частиц должны сохраняться их полное число и полный импульс.

Описание программного кода

Код для модели HPP мы реализовали на языке Julia.

Подключение библиотек и настройка визуализации

using Plots
gr()

• Подключается пакет Plots для построения графиков.

• Выбирается бэкенд gr() для отрисовки.

Константы и параметры модели

const Nx, Ny = 10, 10
const dx = [1, 0, -1, 0]
const dy = [0, 1, 0, -1]
const dir_colors = [:red, :blue, :green, :purple]

• Nx, Ny - размеры внутренней области решетки (без фиктивных узлов).

• dx, dy - массивы смещений по x и y для четырёх направлений движения частиц: вправо, вверх, влево, вниз.

• dir_colors - цвета для визуализации направлений частиц.

Создание пустой сетки

function create_grid()
    zeros(Bool, Nx+2, Ny+2, 4)
end

• Создаётся булев массив размером (Nx+2, Ny+2, 4).

• Nx+2 и Ny+2 - учитывают фиктивные узлы по краям (по одному ряду с каждой стороны).

• Последнее измерение 4 - количество направлений движения частиц.

• Все значения изначально false (нет частиц).

Добавление частицы в сетку

function add_particle!(grid, x, y, d)
    @assert 1 ≤ x ≤ Nx && 1 ≤ y ≤ Ny "Particle must be inside physical domain"
    @assert 1 ≤ d ≤ 4 "Direction must be between 1 and 4"
    grid[x+1, y+1, d] = true
end

• Добавляет частицу в позицию (x, y) с направлением d.

• x+1, y+1 - сдвиг на 1 из-за фиктивных узлов.

• Проверяется корректность координат и направления.

Применение периодических граничных условий

function apply_periodic_boundaries!(grid)
    for d in 1:4
        # левая фиктивная = правая физическая
        grid[1, 2:Ny+1, d] .= grid[Nx+1, 2:Ny+1, d]     
        # правая фиктивная = левая физическая
        grid[Nx+2, 2:Ny+1, d] .= grid[2, 2:Ny+1, d]     
        # нижняя фиктивная = верхняя физическая
        grid[2:Nx+1, 1, d] .= grid[2:Nx+1, Ny+1, d]     
        # верхняя фиктивная = нижняя физическая
        grid[2:Nx+1, Ny+2, d] .= grid[2:Nx+1, 2, d]     
    end
end

• Для каждого направления d копирует значения с противоположных физических границ в фиктивные узлы.

• Обеспечивает периодичность: частицы, выходящие с одной границы, появляются с противоположной.

Обработка столкновений частиц

function collide!(grid)
    for x in 2:Nx+1, y in 2:Ny+1
        right, up, left, down = grid[x,y,1], 
                                grid[x,y,2], 
                                grid[x,y,3], 
                                grid[x,y,4]
        if right && left && !up && !down
            grid[x,y,1] = false
            grid[x,y,3] = false
            grid[x,y,2] = true
            grid[x,y,4] = true
        elseif up && down && !right && !left
            grid[x,y,2] = false
            grid[x,y,4] = false
            grid[x,y,1] = true
            grid[x,y,3] = true
        end
    end
end

• Проходит по всем физическим узлам.

• Проверяет столкновения:

  • Лобовое: если есть частицы вправо и влево, меняет их направления на вверх и вниз.

  • Под прямым углом: если есть частицы вверх и вниз, меняет направления на вправо и влево.

• Другие случаи столкновений не обрабатываются (частицы проходят без изменений).

Распространение частиц

function propagate!(grid)
    new_grid = zeros(Bool, size(grid))
    for x in 2:Nx+1, y in 2:Ny+1, d in 1:4
        if grid[x, y, d]
            nx, ny = x + dx[d], y + dy[d]
            new_grid[nx, ny, d] = true
        end
    end
    return new_grid
end

• Создаёт новую пустую сетку.

• Для каждой частицы вычисляет новую позицию, смещая по направлению d.

• Записывает частицу в новую позицию.

• Возвращает обновлённую сетку.

Подсчёт числа частиц

function count_particles(grid)
    sum(grid[2:Nx+1, 2:Ny+1, :])
end

• Считает общее количество частиц во всех направлениях во всех физических узлах.

Вычисление суммарного импульса

function calculate_momentum(grid)
    px, py = 0, 0
    for x in 2:Nx+1, y in 2:Ny+1
        # движение вправо минус влево
        px += grid[x,y,1] - grid[x,y,3]
        # движение вверх минус вниз
        py += grid[x,y,2] - grid[x,y,4]
    end
    return (px, py)
end

• Суммирует по всем узлам разницу частиц, движущихся в противоположных направлениях, по осям X и Y.

• Возвращает вектор импульса.

Визуализация состояния решетки

function plot_grid(grid, step)
    p = heatmap(0:Nx+1, 0:Ny+1, zeros(Nx+2, Ny+2),
        c=:white, aspect_ratio=1, legend=false,
        xlims=(0.5, Nx+1.5), ylims=(0.5, Ny+1.5),
        title="HPP Model (Step $step)")

    plot!(p, [0.5, Nx+1.5, Nx+1.5, 0.5, 0.5], 
             [0.5, 0.5, Ny+1.5, Ny+1.5, 0.5],
          color=:black, linewidth=2, label="")

    for x in 2:Nx+1, y in 2:Ny+1, d in 1:4
        if grid[x, y, d]
            quiver!(p, [x], [y], quiver=([dx[d]*0.4], 
                                         [dy[d]*0.4]),
                   color=dir_colors[d], lw=2, arrow=true)
        end
    end

    return p
end

• Создаёт белый холст с размерами решетки.

• Рисует чёрную рамку вокруг области.

• Для каждой частицы рисует стрелку в направлении движения с цветом, соответствующим направлению.

• Возвращает объект графика.

Запуск всех тестов

function run_all_tests()
    println("Running single particle test...")
    test_single_particle()

    println("Running head-on collision test...")
    test_head_on_collision()

    println("Running right angle collision test...")
    test_right_angle_collision()

    println("All tests completed! Check generated GIFs.")
end

run_all_tests()

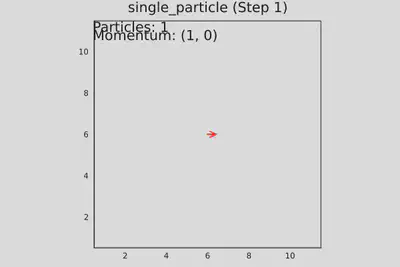
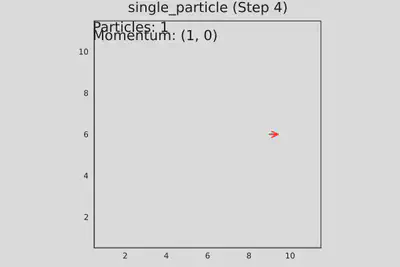
• test_single_particle() - одна частица в центре движется вправо, проверяется распространение и периодичность.

# Тест 1: Одна частица
function test_single_particle()
    grid = create_grid()
    # Частица в центре, движется вправо
    add_particle!(grid, Nx÷2, Ny÷2, 1)  
    
    anim = @animate for step in 1:20
        apply_periodic_boundaries!(grid)
        collide!(grid)
        p = plot_grid(grid, step)
        grid = propagate!(grid)
        
        n = count_particles(grid)
        px, py = calculate_momentum(grid)
        annotate!(p, 0.5, Ny+1.2, text("Particles: $n", :left))
        annotate!(p, 0.5, Ny+0.8, text("Momentum: ($px, $py)", :left))
        
        p
    end
    
    gif(anim, "hpp_single_particle.gif", fps=2)
end

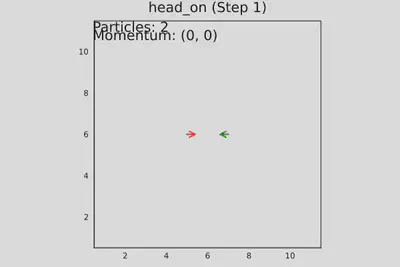
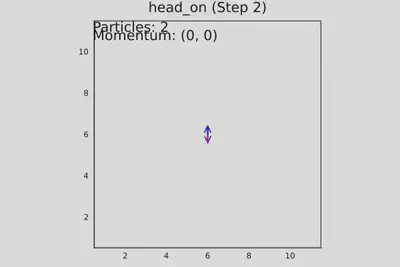
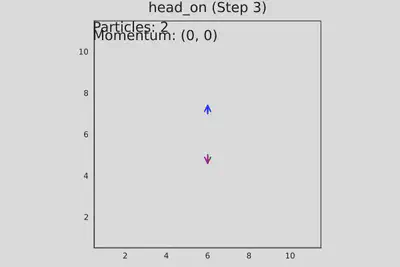
• test_head_on_collision() - две частицы движутся навстречу, проверяется лобовое столкновение.

# Тест 2: Две частицы (лобовое столкновение)
function test_head_on_collision()
    grid = create_grid()
    add_particle!(grid, 4, 5, 1)  # →
    add_particle!(grid, 6, 5, 3)  # ←
    
    anim = @animate for step in 1:10
        apply_periodic_boundaries!(grid)
        collide!(grid)
        p = plot_grid(grid, step)
        grid = propagate!(grid)
        
        n = count_particles(grid)
        px, py = calculate_momentum(grid)
        annotate!(p, 0.5, Ny+1.2, text("Particles: $n", :left))
        annotate!(p, 0.5, Ny+0.8, text("Momentum: ($px, $py)", :left))
        
        p
    end
    
    gif(anim, "hpp_head_on.gif", fps=1)
end

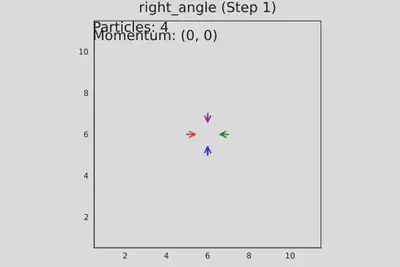
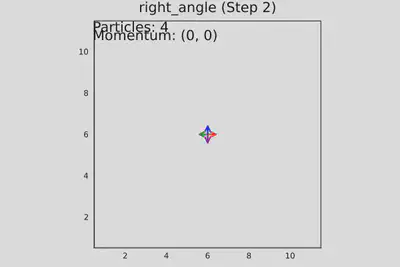
• test_right_angle_collision() - четыре частицы движутся навстречу под прямым углом, проверяется корректность столкновений.

# Тест 3: Четыре частицы (столкновение под прямым углом)
function test_right_angle_collision()
    grid = create_grid()
    add_particle!(grid, 5, 4, 2)  # ↑
    add_particle!(grid, 5, 6, 4)  # ↓
    add_particle!(grid, 4, 5, 1)  # →
    add_particle!(grid, 6, 5, 3)  # ←
    
    anim = @animate for step in 1:10
        apply_periodic_boundaries!(grid)
        collide!(grid)
        p = plot_grid(grid, step)
        grid = propagate!(grid)
        
        n = count_particles(grid)
        px, py = calculate_momentum(grid)
        annotate!(p, 0.5, Ny+1.2, text("Particles: $n", :left))
        annotate!(p, 0.5, Ny+0.8, text("Momentum: ($px, $py)", :left))
        
        p
    end
    
    gif(anim, "hpp_right_angle.gif", fps=1)
end

В каждом тесте:

• Создаётся сетка.

• Добавляются частицы.

• В цикле на каждом шаге применяются граничные условия, столкновения, визуализация и распространение.

• Считается число частиц и импульс.

• Создаётся анимация и сохраняется в GIF.

Заключительная часть

Заключение

Модели решеточных газов $(LGA)$ и решеточное уравнение Больцмана $(LBE)$ представляют собой эффективные инструменты для моделирования газовых потоков. В данной части проекта мы рассмотрели простую базовую модель $HPP$.

Реализовали двумерную модель решеточного газа HPP с четырьмя направлениями движения, периодическими граничными условиями, обработкой столкновений и визуализацией. Тесты демонстрируют корректность работы модели и сохранение физических величин (число частиц и импульс).

Выводы

Во время выполнения третьего этапа группового проекта мы описали и реализовали модель HPP - базовую модель решеточных газов (LGA), которая может быть использована для моделирования решеточного уравнения Больцмана.

Список литературы

1. Медведев Д.А. и др. Моделирование физических процессов и явлений на ПК: Учеб. пособие. // Новосибирск: Новосиб. гос. ун-т, 2010. 101 с.

2. Куперштох А. Л. Моделирование течений с границами раздела жидкость-пар методом решеточных уравнениях Больцмана // Вестник НГУ. Сер. Математика, механика и информатика. 2005. Т. 5, № 3. с. 29–42.

3. Chen S., Lee M., Zhao K. H., Doolen G. D. A lattice gas model with temperature // Physica D. 1989. V. 37. p. 42–59.

4. Чащин Г.С. Метод решёточных уравнений Больцмана: моделирование изотермических низкоскоростных течений // Препринты ИПМ им. М.В.Келдыша. 2021. № 99. 31 с..

5. Frisch, Uriel, Brosl Hasslacher, and Yves Pomeau. “Lattice Gas Automata for the Navier-Stokes Equation.” Phys. Rev. Lett. 56, no. 14 (1986): 1505-1508.

6. Succi, Sauro. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. Oxford University Press, 2001.