Введение

Цель проекта

Разработать и проанализировать модель на основе решеточного уравнения Больцмана для описания течений газа.

Задачи второго этапа проекта

1. Исследовать алгоритмы решения задачи

Актуальность

Моделирование газовых потоков и жидкостей традиционными методами требует значительных вычислительных ресурсов. В связи с этим, методы решеточных газов (LGA) и решеточного уравнения Больцмана (LBE) становятся все более актуальными. Они позволяют упростить вычисления, сохраняя при этом физическую достоверность, и находят применение в различных областях, от гидродинамики до биофизики. В данном докладе мы рассмотрим основные алгоритмы и модели, используемые для решения задач с применением LGA и LBE.

Основная часть

Модель HPP (Hardy–Pomeau–Pazzis)

Модель HPP (Hardy-Pomeau-Pazzis) — это базовая модель решеточных газов (LGA), используемая для моделирования гидродинамических явлений на микроскопическом уровне. Она представляет собой дискретную систему, где пространство и время дискретизованы, а частицы двигаются по узлам квадратной решетки.

Основные характеристики модели HPP:

1. Решетка: используется двумерная квадратная решетка, где узлы расположены на одинаковом расстоянии друг от друга.

2. Частицы: в каждом узле решетки могут находиться частицы единичной массы. Каждая частица может двигаться в одном из четырех направлений: вверх, вниз, вправо или влево.

3. Скорость: все частицы имеют одинаковую скорость, направленную к соседнему узлу. Расстояние между узлами ($\Delta x$) и шаг времени ($\Delta t$) выбираются так, чтобы частица могла переместиться в соседний узел за один временной шаг.

4. Принцип исключения: в каждом узле может находиться не более одной частицы, движущейся в заданном направлении.

5. Этапы эволюции:

   • Распространение (Streaming): частицы перемещаются в соседние узлы в соответствии со своими скоростями. За один шаг времени частица переходит в соседний узел в направлении своего движения.
   • Столкновения (Collision): в узлах происходят столкновения частиц, при которых сохраняются количество частиц и полный импульс.

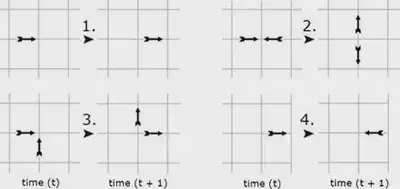
6. Правила столкновений: столкновения происходят таким образом, чтобы выполнялись законы сохранения. В модели HPP нетривиальные столкновения происходят, когда две частицы движутся навстречу друг другу (почти “лоб в лоб”). После столкновения частицы меняют направления движения на 90 градусов. Во всех остальных случаях столкновения считаются несущественными, и частицы продолжают двигаться в прежних направлениях.

7. Кодирование состояний: состояние каждого узла решетки кодируется битами. Поскольку имеется четыре возможных направления движения, для кодирования состояния узла требуется четыре бита. Каждый бит соответствует одному из направлений: 0 — нет частицы, 1 — есть частица, движущаяся в этом направлении. Например, если частицы движутся вправо и вверх, состояние узла кодируется как 0101 в двоичном формате.

Математическое описание:

Обозначим возможные направления скорости как $d_1, d_2, d_3, d_4$$. Тогда:

• $d_1 = 0001_2 = 1$

• $d_2 = 0010_2 = 2$

• $d_3 = 0100_2 = 4$

• $d_4 = 1000_2 = 8$

Основные операции для работы с состояниями узлов:

1. Добавление частицы: добавление к состоянию $S$ частицы с направлением скорости $d_k$: $$ S \text{ OR } d_k \rightarrow S $$

2. Проверка наличия частицы: проверка, есть ли в состоянии $S$ частица с направлением скорости $d_k$: $$ \text{if } (S \text{ AND } d_k) \neq 0 $$ Если результат не равен 0, то частица с направлением $d_k$ присутствует в узле.

Недостатки модели HPP:

1. Отсутствие симметрии: квадратная решетка с четырьмя направлениями скорости недостаточно симметрична, что приводит к анизотропии в макроскопических свойствах.

2. Нефизичное поведение: модель HPP неточно описывает гидродинамические свойства жидкостей и газов.

Для устранения этих недостатков были разработаны более совершенные модели, такие как FHP (Frisch-Hasslacher-Pomeau) на треугольных решетках и модели с добавлением покоящихся частиц.

Модель FHP-I (Frisch-Hasslacher-Pomeau)

Модель FHP-I (Frisch-Hasslacher-Pomeau) — это улучшенная модель решеточных газов (LGA), разработанная для устранения недостатков модели HPP, связанных с недостаточной симметрией. В модели FHP-I используется треугольная сетка и шесть направлений скорости.

Основные характеристики модели FHP-I:

1. Решетка: используется двумерная треугольная решетка, где каждый узел имеет шесть ближайших соседних узлов, расположенных под углами 60 градусов друг к другу.

2. Частицы: в каждом узле решетки могут находиться частицы единичной массы. Каждая частица может двигаться в одном из шести направлений к соседним узлам.

3. Скорость: все частицы имеют одинаковую скорость, направленную к соседнему узлу. Как и в модели HPP, расстояние между узлами и шаг времени выбираются так, чтобы частица могла переместиться в соседний узел за один временной шаг.

4. Принцип исключения: в каждом узле может находиться не более одной частицы, движущейся в заданном направлении.

5. Этапы эволюции:

   • Распространение (Streaming): частицы перемещаются в соседние узлы в соответствии со своими скоростями.
   • Столкновения (Collision): в узлах происходят столкновения частиц, при которых сохраняются количество частиц и полный импульс.

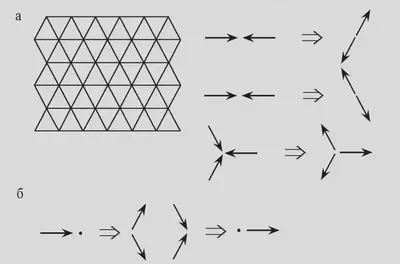
6. Правила столкновений: столкновения происходят таким образом, чтобы выполнялись законы сохранения. Важным аспектом модели FHP-I является наличие нескольких типов столкновений, обеспечивающих сохранение массы и импульса. Примеры столкновений:

   • Две частицы, движущиеся навстречу друг другу, могут изменить направление на 60 градусов.
   • Три частицы, движущиеся по трем направлениям, могут изменить направления так, чтобы общий импульс остался неизменным.

7. Кодирование состояний: состояние каждого узла решетки кодируется битами. Поскольку имеется шесть возможных направлений движения, для кодирования состояния узла требуется шесть битов. Каждый бит соответствует одному из направлений: 0 — нет частицы, 1 — есть частица, движущаяся в этом направлении.

Преимущества модели FHP-I:

1. Улучшенная симметрия: треугольная решетка с шестью направлениями скорости обладает большей симметрией по сравнению с квадратной решеткой модели HPP. Это позволяет получить более точное описание гидродинамических свойств.

2. Реалистичное поведение: модель FHP-I более точно описывает гидродинамические свойства жидкостей и газов по сравнению с моделью HPP.

Недостатки модели FHP-I:

1. Сложность реализации: треугольная решетка и более сложные правила столкновений делают реализацию модели FHP-I более сложной по сравнению с моделью HPP.

Модель FHP-III

Модель FHP-III — это расширение модели FHP-I, предназначенное для улучшения её физических свойств за счет добавления покоящихся частиц. Введение покоящихся частиц позволяет более точно моделировать гидродинамические явления и улучшить изотропность модели.

Основные характеристики модели FHP-III:

1. Решетка: используется двумерная треугольная решетка, как и в модели FHP-I. Каждый узел имеет шесть ближайших соседних узлов, расположенных под углами 60 градусов друг к другу.

2. Частицы: в каждом узле решетки могут находиться частицы единичной массы. В отличие от FHP-I, в FHP-III добавлены покоящиеся частицы, которые не двигаются между узлами. Таким образом, у нас есть шесть движущихся частиц и покоящаяся частица.

3. Скорость: шесть движущихся частиц имеют одинаковую скорость, направленную к соседнему узлу. Покоящиеся частицы имеют нулевую скорость.

4. Принцип исключения: в каждом узле может находиться не более одной частицы, движущейся в заданном направлении, и не более одной покоящейся частицы.

5. Этапы эволюции:

   • Распространение (Streaming): движущиеся частицы перемещаются в соседние узлы в соответствии со своими скоростями. Покоящиеся частицы остаются на месте.
   • Столкновения (Collision): в узлах происходят столкновения частиц, при которых сохраняются количество частиц и полный импульс. В FHP-III добавляются новые правила столкновений, учитывающие покоящиеся частицы.

6. Правила столкновений: столкновения происходят таким образом, чтобы выполнялись законы сохранения. Некоторые примеры столкновений:

   • Две частицы, движущиеся навстречу друг другу, могут изменить направление на 60 градусов (как в FHP-I).
   • Частица может столкнуться с покоящейся частицей, изменив направление своего движения.
   • Покоящаяся частица может быть создана или уничтожена в результате столкновений.

7. Кодирование состояний: состояние каждого узла решетки кодируется битами. Поскольку имеется шесть возможных направлений движения и возможность наличия покоящейся частицы, для кодирования состояния узла требуется семь битов. Шесть битов соответствуют направлениям движения, а один бит — наличию покоящейся частицы.

Преимущества модели FHP-III:

1. Улучшенная изотропность: добавление покоящихся частиц улучшает изотропность модели, что позволяет получить более точное описание гидродинамических свойств.

2. Более реалистичное поведение: модель FHP-III более точно описывает гидродинамические свойства жидкостей и газов по сравнению с моделями HPP и FHP-I.

Недостатки модели FHP-III:

1. Сложность реализации: добавление покоящихся частиц и новых правил столкновений делает реализацию модели FHP-III более сложной по сравнению с моделями HPP и FHP-I.

Модель с 9 направлениями скорости является модификацией модели решеточных газов, предназначенной для улучшения изотропности и введения понятия температуры в систему. Она использует квадратную сетку, но расширяет возможные направления движения частиц, позволяя им перемещаться не только по горизонтали и вертикали, но и по диагонали. Кроме того, вводится понятие покоящихся частиц.

Модель с 9 направлениями скорости

Основные характеристики модели с 9 направлениями скорости:

1. Решетка: используется двумерная квадратная решетка, как и в модели HPP.

2. Частицы: в каждом узле решетки могут находиться частицы, движущиеся в одном из восьми направлений (вверх, вниз, вправо, влево, и по четырем диагоналям), а также покоящиеся частицы.

3. Скорость:

   • Частицы, движущиеся по горизонтали и вертикали, имеют скорость $v_1 = 1$.
   • Частицы, движущиеся по диагонали, имеют скорость $v_2 = \sqrt{2}$.
   • Покоящиеся частицы имеют нулевую скорость.

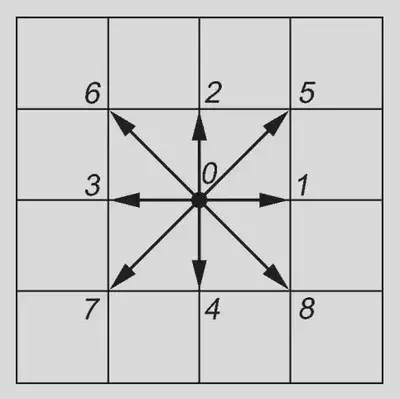
4. Направления движения:

   • 4 направления с единичной скоростью: вправо, влево, вверх, вниз.
   • 4 направления с диагональной скоростью: вправо-вверх, вправо-вниз, влево-вверх, влево-вниз.
   • 1 состояние покоя.

5. Этапы эволюции:

   • Распространение (Streaming): частицы перемещаются в соседние узлы в соответствии со своими скоростями.
   • Столкновения (Collision): в узлах происходят столкновения частиц, при которых сохраняются количество частиц, импульс и энергия.

6. Правила столкновений: правила столкновений должны обеспечивать сохранение массы, импульса и энергии. Это достигается за счет более сложных правил столкновений по сравнению с моделями HPP и FHP.

7. Кодирование состояний: состояние каждого узла решетки кодируется битами. Поскольку имеется 9 возможных состояний (8 направлений движения и состояние покоя), для кодирования состояния узла требуется 9 битов.

Физические параметры:

В модели с 9 направлениями скорости можно определить макроскопические параметры, такие как плотность, полная энергия и температура.

1. Плотность ($\rho$): $$\rho = n_0 + n_1 + n_2$$

   • $n_0$ — число покоящихся частиц.

   • $n_1$ — число частиц с единичной скоростью.

   • $n_2$ — число частиц со скоростью $\sqrt{2}$.

2. Полная энергия ($E$): $$E = P + \frac{\rho u^2}{2} = \sum_i n_i \frac{v_i^2}{2} = \frac{n_1}{2} + n_2$$

   • $P$ — давление.

   • $u$ — макроскопическая скорость.

3. Температура ($T$): $T = \frac{P}{\rho}$

Преимущества модели с 9 направлениями скорости:

1. Изотропность: добавление диагональных направлений движения улучшает изотропность модели по сравнению с моделью HPP.

2. Возможность введения температуры: наличие различных скоростей позволяет ввести понятие температуры, что важно для моделирования тепловых процессов.

3. Более реалистичное поведение: модель с 9 направлениями скорости более точно описывает гидродинамические свойства жидкостей и газов по сравнению с более простыми моделями.

Недостатки модели с 9 направлениями скорости:

1. Сложность реализации: добавление новых направлений движения и покоящихся частиц усложняет реализацию модели по сравнению с моделями HPP и FHP.

2. Вычислительные затраты: большее число состояний и более сложные правила столкновений увеличивают вычислительные затраты.

Решеточное уравнение Больцмана (LBE, Lattice Boltzmann Equation)

Решеточное уравнение Больцмана (LBE) — это вычислительный метод, используемый для моделирования широкого спектра физических процессов, включая гидродинамику, фазовые переходы и химические реакции. LBE является более общим подходом по сравнению с моделями решеточных газов (LGA), такими как HPP, FHP-I и FHP-III, и предоставляет более точное и гибкое средство моделирования сложных систем.

Основные характеристики LBE:

1. Дискретизация пространства и времени: LBE, как и LGA, дискретизует пространство и время. Пространство представляется в виде решетки (обычно квадратной или треугольной), а время разбивается на дискретные шаги.

2. Функция распределения: в отличие от LGA, где отслеживаются отдельные частицы, LBE работает с функцией распределения $f_k(x, t)$, которая описывает вероятность нахождения частиц в узле $x$ в момент времени $t$, движущихся в направлении $k$.

3. Скорости: частицы могут двигаться в нескольких дискретных направлениях $c_k$, определяемых геометрией решетки.

4. Основное уравнение: эволюция системы описывается уравнением:

   $$ f_k(x + c_k \Delta t, t + \Delta t) = f_k(x, t) + \Omega_k(x, t) $$

   • $f_k(x, t)$ — одночастичная функция распределения.

   • $c_k$ — скорость частиц.

   • $\Omega_k(x, t)$ — столкновительный член, описывающий изменения функции распределения из-за столкновений частиц.

5. Столкновительный член: описывает, как частицы взаимодействуют друг с другом. Наиболее часто используется модель BGK (Bhatnagar-Gross-Krook):

   $$ \Omega_k = \frac{1}{\tau}(f_k^{eq} - f_k) $$

   • $\tau$ — время релаксации, характеризующее скорость приближения системы к равновесию.

   • $f_k^{eq}$ — равновесная функция распределения, описывающая состояние системы в равновесии.

6. Равновесная функция распределения: обычно выбирается в виде разложения по полиномам Эрмита или в другом подходящем виде, чтобы обеспечить выполнение законов сохранения. Например, для модели D2Q9 (двумерная модель с 9 скоростями) равновесная функция распределения может быть записана как:

   $$ f_k^{eq} = w_k \rho \left[1 + \frac{c_k \cdot u}{c_s^2} + \frac{(c_k \cdot u)^2}{2c_s^4} - \frac{u^2}{2c_s^2}\right] $$

   • $w_k$ — весовые коэффициенты, зависящие от направления скорости.
   • $\rho$ — плотность.
   • $u$ — макроскопическая скорость.
   • $c_s$ — скорость звука в решеточной модели.

7. Макроскопические параметры: макроскопические параметры, такие как плотность и скорость, вычисляются через функции распределения:

   $$ \rho = \sum_k f_k $$

   $$ \rho u = \sum_k f_k c_k $$

Преимущества LBE:

1. Гибкость: LBE может быть использован для моделирования широкого спектра физических явлений, включая гидродинамику, теплопередачу, фазовые переходы, химические реакции и многофазные потоки.
2. Эффективность: LBE обладает хорошей параллелизуемостью, что позволяет эффективно использовать многопроцессорные системы для моделирования больших систем.
3. Точность: LBE обеспечивает более точное описание гидродинамических свойств по сравнению с более простыми моделями LGA.
4. Простота реализации граничных условий: LBE позволяет легко реализовывать сложные граничные условия.

Недостатки LBE:

1. Ограничения по скорости: LBE обычно работает хорошо для низкоскоростных течений. Для моделирования высокоскоростных течений требуются специальные модификации.
2. Вычислительные затраты: LBE требует больше вычислительных ресурсов по сравнению с простыми моделями LGA.

Применение LBE:

LBE находит широкое применение в различных областях науки и техники, включая:

1. Гидродинамика: моделирование течений жидкостей и газов в сложных геометриях.
2. Аэродинамика: моделирование обтекания тел потоками воздуха.
3. Пористые среды: моделирование течений в пористых материалах.
4. Медицина: моделирование кровотока в сосудах.
5. Химическая инженерия: моделирование химических реакций в растворах.
6. Моделирование фазовых переходов: моделирование процессов конденсации, испарения и кристаллизации.

Модель с взаимодействием между частицами используется для моделирования фазовых переходов и разделения фаз. В этой модели к обычным алгоритмам решеточных газов или решеточного уравнения Больцмана добавляются силы, действующие между частицами, находящимися в разных узлах решетки.

Модель с взаимодействием между частицами

Основные характеристики модели с взаимодействием между частицами:

1. Взаимодействие между частицами: для описания жидкостей и газов вводятся силы взаимодействия между частицами. Эти силы могут быть как отталкивающими (для моделирования разделения веществ), так и притягивающими (для моделирования фазовых переходов жидкость-газ).

2. Типы взаимодействий:

   • Отталкивание: используется для моделирования разделения смеси веществ на компоненты. Частицы разных компонентов отталкиваются друг от друга, что приводит к их разделению.
   • Притяжение: используется для моделирования фазовых переходов, таких как конденсация пара в жидкость или вскипание перегретой жидкости. Частицы притягиваются друг к другу, образуя кластеры или капли.

3. Влияние внешних сил: внешние силы могут быть учтены через изменение скорости частиц: $$ \Delta u = \frac{F \Delta t}{\rho} $$

   • $\Delta u$ — изменение скорости.
   • $F$ — внешняя сила.
   • $\Delta t$ — шаг времени.
   • $\rho$ — плотность.

   Уравнение Больцмана модифицируется добавкой:

   $$ f_k(x + c_k \Delta t, t + \Delta t) = f_k(x, t) + \Omega_k(x, t) + \Delta f_k $$

   где:

   $$ \Delta f_k = f_k^{eq}(\rho, u + \Delta u) - f_k^{eq}(\rho, u) $$

   • $\Delta f_k$ — изменение функции распределения, вызванное внешней силой.
   • $f_k^{eq}$ — равновесная функция распределения.

4. Моделирование фазовых переходов: фазовые переходы моделируются через силы притяжения между соседними узлами:

   $$ F(x) = \psi(\rho(x)) \sum_{k} G_k e_k \psi(\rho(x + e_k)) $$

   • $F(x)$ — сила, действующая на узел $x$.
   • $\psi(\rho(x))$ — функция, зависящая от плотности в узле $x$.
   • $G_k > 0$ — константа, определяющая силу притяжения.
   • $e_k$ — вектор, указывающий направление к соседнему узлу.

Алгоритм моделирования с взаимодействием:

1. Инициализация:

   • Создание решетки (квадратной или треугольной).
   • Установка начальных условий (плотность, скорость, температура).
   • Определение параметров взаимодействия (сила притяжения или отталкивания).

2. Распространение (Streaming): частицы перемещаются в соседние узлы в соответствии со своими скоростями.

3. Вычисление сил взаимодействия: для каждого узла вычисляется сила, действующая на него со стороны соседних узлов.

4. Столкновения (Collision): в узлах происходят столкновения частиц, при которых сохраняются количество частиц, импульс и энергия. Учитывается влияние сил взаимодействия на изменение скоростей частиц.

5. Обновление скоростей: скорости частиц изменяются под действием сил взаимодействия и внешних сил.

6. Повторение шагов 2-5: процесс повторяется до достижения стационарного состояния или заданного времени моделирования.

Применение:

• Моделирование конденсации и испарения: позволяет изучать процессы образования капель из пересыщенного пара и вскипания перегретой жидкости.

• Разделение фаз (спинодальная декомпозиция): моделирование разделения смеси на фазы с разными свойствами.

• Моделирование многофазных потоков: изучение течений, в которых одновременно присутствуют несколько фаз (например, жидкость и газ).

Модель с несколькими компонентами используется

Модель с несколькими компонентами используется для моделирования смесей веществ и химических реакций. В этой модели каждый компонент представлен своим набором частиц или функций распределения, и учитываются взаимодействия между различными компонентами.

Основные характеристики модели с несколькими компонентами:

1. Несколько типов частиц: в системе присутствует несколько видов частиц, каждый из которых соответствует определенному компоненту смеси.

2. Функции распределения для каждого компонента: если используется подход LBE, то для каждого компонента определяется своя функция распределения $f_{k,i}(x, t)$, где $i$ — индекс компонента.

3. Взаимодействия между компонентами: учитываются силы взаимодействия между различными компонентами смеси. Эти силы могут быть как отталкивающими (для моделирования разделения фаз), так и притягивающими (для моделирования образования соединений).

4. Химические реакции: в модели могут быть реализованы химические реакции между компонентами. Для этого вводятся правила, определяющие, как и с какой вероятностью частицы разных компонентов могут превращаться друг в друга.

5. Уравнения эволюции: эволюция системы описывается набором уравнений, учитывающих как гидродинамические процессы, так и химические реакции.

Алгоритм моделирования с несколькими компонентами:

1. Инициализация:

   • Создание решетки (квадратной или треугольной).
   • Установка начальных условий (плотность, скорость, концентрация каждого компонента).
   • Определение параметров взаимодействия между компонентами.
   • Задание правил химических реакций (если они есть).

2. Распространение (Streaming): частицы каждого компонента перемещаются в соседние узлы в соответствии со своими скоростями.

3. Вычисление сил взаимодействия: для каждого узла вычисляются силы, действующие на частицы каждого компонента со стороны других компонентов.

4. Столкновения (Collision): в узлах происходят столкновения частиц, при которых сохраняются количество частиц, импульс и энергия для каждого компонента. Учитывается влияние сил взаимодействия на изменение скоростей частиц.

5. Химические реакции: в узлах происходят химические реакции между компонентами в соответствии с заданными правилами. В результате этих реакций изменяется количество частиц каждого компонента.

6. Обновление скоростей: скорости частиц каждого компонента изменяются под действием сил взаимодействия и внешних сил.

7. Повторение шагов 2-6: процесс повторяется до достижения стационарного состояния или заданного времени моделирования.

Математическое описание:

Для LBE с несколькими компонентами уравнение эволюции выглядит следующим образом:

$$ f_{k,i}(x + c_k \Delta t, t + \Delta t) = f_{k,i}(x, t) + \Omega_{k,i}(x, t) $$

• $f_{k,i}(x, t)$ — функция распределения для компонента $i$ в узле $x$ в момент времени $t$.
• $c_k$ — скорость частиц.
• $\Omega_{k,i}(x, t)$ — столкновительный член, описывающий изменения функции распределения из-за столкновений и химических реакций.

Столкновительный член может включать в себя как релаксацию к равновесию, так и члены, описывающие химические реакции:

$$ \Omega_{k,i} = \Omega_{k,i}^{collision} + \Omega_{k,i}^{reaction} $$

Применение:

• Моделирование смешивания жидкостей: позволяет изучать процессы смешивания различных жидкостей и газов.

• Разделение веществ: моделирование разделения смеси на компоненты (например, разделение нефти на фракции).

• Моделирование химических реакций: изучение кинетики химических реакций в растворах и газах.

• Реакция-диффузия: моделирование процессов, в которых химические реакции сочетаются с диффузией веществ.

Заключительная часть

Заключение

Модели решеточных газов $(LGA)$ и решеточное уравнение Больцмана $(LBE)$ представляют собой эффективные инструменты для моделирования газовых потоков, требующие меньше вычислительных ресурсов по сравнению с традиционными методами.

Различные модели обладают разными характеристиками и применимы для разных задач. $HPP$ — простая базовая модель, $FHP-I$ и $FHP-III$ улучшают симметрию и изотропность, а модель с 9 направлениями скорости позволяет вводить понятие температуры. $LBE$ является наиболее общим и гибким подходом.

Выбор конкретного алгоритма зависит от требований к точности, вычислительным ресурсам и специфике решаемой задачи.

Выводы

Во время выполнения второго этапа группового проекта мы сделали теоретическое описание алгоитмов, которые могут быть использованы для моделирования решеточного уравнения Больцмана.

Список литературы

1. Медведев Д.А. и др. Моделирование физических процессов и явлений на ПК: Учеб. пособие. // Новосибирск: Новосиб. гос. ун-т, 2010. 101 с.

2. Куперштох А. Л. Моделирование течений с границами раздела жидкость-пар методом решеточных уравнениях Больцмана // Вестник НГУ. Сер. Математика, механика и информатика. 2005. Т. 5, № 3. с. 29–42.

3. Chen S., Lee M., Zhao K. H., Doolen G. D. A lattice gas model with temperature // Physica D. 1989. V. 37. p. 42–59.

4. Чащин Г.С. Метод решёточных уравнений Больцмана: моделирование изотермических низкоскоростных течений // Препринты ИПМ им. М.В.Келдыша. 2021. № 99. 31 с..

5. Frisch, Uriel, Brosl Hasslacher, and Yves Pomeau. “Lattice Gas Automata for the Navier-Stokes Equation.” Phys. Rev. Lett. 56, no. 14 (1986): 1505-1508.

6. Succi, Sauro. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. Oxford University Press, 2001.