Введение

Цель проекта

Разработать и проанализировать модель на основе решеточного уравнения Больцмана для описания течений газа.

Задачи первого этапа проекта

1. Формулировка научной проблемы: определение ключевых аспектов проблемы и ее значимости.
2. Теоретическое описание задачи: формулировка теоретических основ модели.
3. Описание модели: разработка математической модели, отражающей основные физические процессы.

Объект и предмет исследования

• Объект: физические процессы в газах и жидкостях.
• Предмет: использование решеточных методов (LGA и LBE) для описания динамики частиц на дискретной сетке.

Постановка проблемы

Моделирование газовых потоков и жидкостей традиционными методами, такими как уравнения Навье-Стокса и методы конечных разностей, требует значительных вычислительных ресурсов и сложных алгоритмов. Методы решеточных газов (Lattice-Gas Automata, LGA) и решеточного уравнения Больцмана (Lattice Boltzmann Equation, LBE) предлагают альтернативу, позволяя упростить вычисления при сохранении физической достоверности. Эти методы широко используются в различных областях:

• Гидродинамика: моделирование течений жидкостей и газов.
• Аэродинамика: изучение воздушных потоков и аэродинамических свойств объектов.
• Биофизика: моделирование биологических систем и процессов.
• Моделирование пористых материалов: изучение свойств и поведения пористых сред.
• Анимация визуальных эффектов: создание реалистичных симуляций жидкостей и газов в кино и играх.

Применение методов актуально для:

1. Исследования сложных многокомпонентных течений: моделирование взаимодействия нескольких жидкостей или газов.
2. Течений с фазовыми переходами и химическими реакциями: изучение процессов, связанных с изменением состояния вещества или химическими реакциями.
3. Создания высокопроизводительных параллельных алгоритмов: разработка эффективных вычислительных методов для крупномасштабных симуляций.

Научная значимость

1. Моделирование сложных систем: решеточные методы позволяют описывать взаимодействие частиц и фазовые переходы, что важно для понимания поведения реальных систем.
2. Высокая скорость вычислений: дискретная природа моделей упрощает распараллеливание и ускоряет вычисления.
3. Простота реализации: алгоритмы не требуют сложных вычислительных схем, что делает их доступными для широкого круга исследователей и инженеров.

Общее описание

В отчете рассматриваются методы моделирования гидродинамических процессов на основе решеточных моделей: Lattice-Gas Automata (LGA) и Lattice Boltzmann Equation (LBE). Эти методы позволяют упростить вычисления и моделировать сложные явления, такие как течения жидкостей и газов, теплопередача и фазовые переходы.

Основная часть

Решеточные газы (LGA)

Общее описание

Рассматривается квадратная решетка, в узлах которой находятся частицы единичной массы. Расстояние между узлами $\Delta x$ и шаг по времени $\Delta t$ принимаются за единицу длины и времени соответственно. В каждом узле может быть не более одной частицы с данным направлением скорости (принцип исключения).

Модель HPP (Hardy–Pomeau–Pazzis)

• Описание:
  • Используется квадратная решетка.
  • Частицы могут двигаться в одном из соседних узлов (вверх, вниз, вправо, влево).
  • Соударения происходят с сохранением количества частиц и их полного импульса.
  • Нетривиальными являются соударения “почти лоб в лоб”, после которых скорости частиц поворачиваются на 90 градусов. В остальных случаях можно считать, что столкновения не произошло (частицы пролетели мимо друг друга).
    • Пояснение: Столкновения “почти лоб в лоб” — это когда частицы летят навстречу друг другу по одной линии, а после столкновения их траектории отклоняются на 90 градусов.

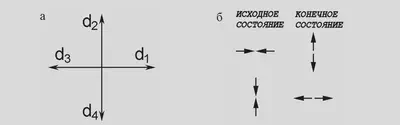
• Кодирование состояний:
  • Наличие частицы, имеющей скорость по каждому направлению, может быть закодировано одним битом (0 — нет частицы, 1 — есть).
  • Так можно записать состояние каждого узла в четырех битах.
  • Примеры операций:
    • Добавление к состоянию S частицы с направлением скорости $d_k$: $S \text{ or } d_k \rightarrow S$
    • Проверка: есть ли в состоянии S частица с направлением скорости $d_k$: $\text{if } (S \text{ and } d_k) \neq 0$
  • Здесь or — двоичная побитовая операция “или”, а and — двоичная операция “и”.
    • Пояснение: Операции or и and используются для манипулирования битами, что позволяет эффективно кодировать и обрабатывать состояния частиц.
  • Все операции сводятся к целочисленной арифметике, это означает высокую скорость расчетов и отсутствие ошибок округления. Кроме того, все вычисления локальные, поэтому их можно выполнять параллельно.
• Недостатки:
  • Квадратная сетка с 4 возможными направлениями скорости частиц недостаточно симметрична.

Модель FHP-I

• Описание:
  • Используется треугольная сетка с 6 возможными направлениями скорости частиц в узле.
  • Обладает большей симметрией по сравнению с моделью HPP.

Модель FHP-III

• Описание:
  • Включает в себя покоящиеся частицы.
  • Геометрия решетки и возможные столкновения частиц для моделей FHP-I, FHP-III представлены ниже:

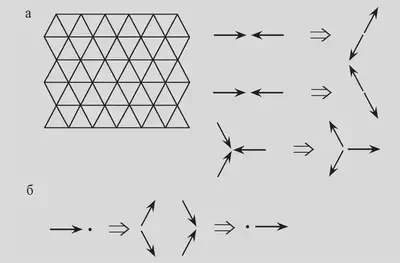
Квадратная решетка с движением по диагоналям

• Описание:
  • Вводится возможность движения частиц по диагоналям (скорость $\sqrt{2}$).
  • Вместе с покоящимися частицами получаем 9 направлений скорости.
  • Так как модули скоростей различны, возможен нетривиальный закон сохранения энергии, и можно ввести температуру.
• Параметры:
  • Число покоящихся частиц: $n_0$
  • Число частиц с единичной скоростью: $n_1$
  • Число частиц со скоростью $\sqrt{2}$: $n_2$
  • Плотность: $\rho = n_0 + n_1 + n_2$
  • Полная энергия: $E = P + \frac{\rho u^2}{2} = \sum_i n_i v_i^2 / 2 = n_1/2 + n_2$ (где $P$ — давление)
  • Температура: $T = \frac{P}{\rho}$
• Возможности:
  • Моделирование течений с переменной температурой.
  • Моделирование теплопередачи и выделения энергии.
  • Легко задавать граничные условия любого вида (например, разворачивать скорости прилетевших частиц на угол 180 градусов на твердых границах). Несколько примеров столкновений, в том числе с выделением энергии, приведены ниже:

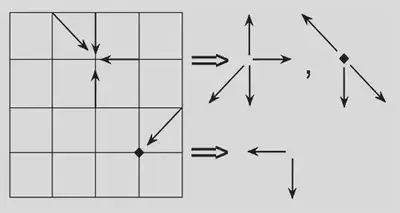
Решеточное уравнение Больцмана (LBE)

Общее описание

Метод LBE позволяет устранить статистический шум, возникающий из-за случайности в модели LGA. Эволюция системы описывается уравнением Больцмана:

$f_k(x + c_k \Delta t, t + \Delta t) = f_k(x, t) + \Omega_k(x, t)$, где:

• $f_k$ — одночастичная функция распределения.

• $c_k$ — скорость частиц.

• $\Omega_k$ — столкновительный член.

  • Пояснение: Это уравнение описывает, как меняется распределение частиц со временем и в пространстве. Левая часть описывает перенос частиц, а правая — изменения из-за столкновений.

• Условие:

  • Скорости частиц $c_k$ должны удовлетворять условию $c_k \Delta t = e_k$, где $e_k$ — векторы, соединяющие узел с соседними. Обычно принимается $\Delta t = 1$.
    • Пояснение: Это условие гарантирует, что частицы перемещаются из одного узла в другой за один временной шаг.

• Макроскопические параметры:

  • Плотность: $\rho = \sum_k f_k$
  • Скорость: $\rho u = \sum_k f_k c_k$
    • Пояснение: Эти формулы позволяют связать микроскопические параметры (функцию распределения) с макроскопическими (плотность и скорость).

• Столкновительный член:

  • Описывает релаксацию системы к равновесному состоянию: $\Omega_k = \frac{1}{\tau} (f_k^{eq} - f_k)$, где $f_k^{eq}$ — равновесные функции распределения.
  • Равновесные функции распределения зависят от плотности и скорости вещества в узле, чтобы выполнялись законы сохранения массы и импульса в столкновениях, то есть $\rho = \sum_k f_k^{eq}, \quad \rho u = \sum_k f_k^{eq} c_k$.
    • Пояснение: Столкновительный член моделирует, как частицы стремятся к равновесному состоянию, а равновесные функции распределения определяют это состояние.

• Кинетическая температура:

  • $\theta = \frac{kT}{m}$ (в энергетических единицах) задается уравнением $\rho \theta = \sum_k f_k^{eq} (c_k - u)^2 / 2$.
    • Пояснение: Кинетическая температура характеризует среднюю кинетическую энергию частиц.
  • Часто масса LBE частиц принимается за единицу, $m = 1$.

• Преимущества:

  • Хорошо описывает течения вязкой жидкости в пределе малых скоростей (число Маха $M = u / c_s \ll 1$).
    • Пояснение: Число Маха — отношение скорости потока к скорости звука.
  • Время релаксации $\tau$ определяет кинематическую вязкость $\nu = (\tau - 1/2) c_s^2 \Delta t$.
  • На твердых границах можно просто разворачивать скорости прилетевших частиц, моделируя непроницаемые стенки без проскальзывания.
    • Пояснение: Граничные условия задаются простым отражением скорости, что упрощает моделирование.

Приложение. Явный вид функций $f_k^{eq}$

Обычно равновесные функции распределения выбираются в максвелловском виде:

$f_k^{eq} \sim \exp(-(c_k - u)^2 / 2\theta)$.

В изотермических моделях достаточно разложить экспоненту в ряд с точностью до членов порядка $u^2$, используя приближенную формулу $e^x = 1 + x/1! + x^2/2! + …$. В результате получаем:

$f_k^{eq} = w_k \rho \left( 1 + \frac{c_k \cdot u}{\theta} + \frac{(c_k \cdot u)^2}{2\theta^2} - \frac{u^2}{2\theta} \right)$.

Коэффициенты $w_k \sim \exp(-c_k^2 / 2\theta)$ зависят только от модуля $|c_k|$.

• Примеры:

  • Одномерная модель:
    • $c_0 = 0, \quad c_{-1} = -h / \Delta t, \quad c_1 = h / \Delta t$
    • $\theta = \frac{1}{3} (h / \Delta t)^2, \quad w_0 = \frac{2}{3}, \quad w_{\pm 1} = \frac{1}{6}$
    • $f_0^{eq} = \frac{2}{3} \rho (1 - \frac{3}{2} \tilde{u}^2), \quad f_{\pm 1}^{eq} = \frac{1}{6} \rho (1 \pm 3\tilde{u} + 3\tilde{u}^2)$
    • Здесь $\tilde{u} = u \Delta t / h$ — безразмерная скорость вещества.
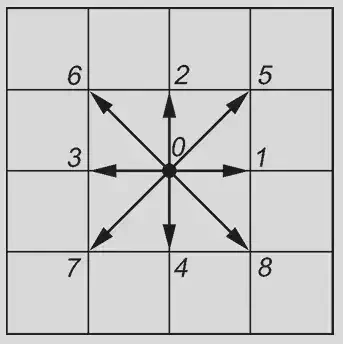
  • Двумерная модель на квадратной сетке с 9 направлениями:
    • $c_0 = (0, 0)$
    • $c_k = \frac{h}{\Delta t} (\cos(k \pi / 2), \sin(k \pi / 2))$ для $k = 1 \dots 4$
    • $c_k = \frac{\sqrt{2} h}{\Delta t} (\cos((k + 1/2) \pi / 2), \sin((k + 1/2) \pi / 2))$ для $k = 5 \dots 8$
    • $\theta = \frac{1}{3} (h / \Delta t)^2, \quad w_0 = \frac{4}{9}, \quad w_{1-4} = \frac{1}{9}, \quad w_{5-8} = \frac{1}{36}$
    • $f_0^{eq} = w_0 \rho (1 - d \tilde{u}^2)$
    • $f_1^{eq} = w_1 \rho (1 + a \tilde{u}_x + b \tilde{u}_x^2 - d \tilde{u}^2)$
    • …
    • $f_8^{eq} = w_8 \rho (1 + a (\tilde{u}_x - \tilde{u}_y) + b (\tilde{u}_x - \tilde{u}_y)^2 - d \tilde{u}^2)$
    • где $a = \frac{(\Delta t / h)^2}{\theta} = 3, \quad b = \frac{(\Delta t / h)^4}{2 \theta^2} = \frac{9}{2}, \quad d = \frac{(\Delta t / h)^2}{2 \theta} = \frac{3}{2}$

Далее для простоты будем опускать значок «~» у переменной $u$.

Модели LGA со взаимодействием между частицами

Общее описание

Приведенные выше модели описывают скорее газ, чем жидкость. В жидкости между частицами существуют силы взаимодействия, проявлением которых являются поверхностное натяжение, а также фазовые переходы жидкость-газ.

• Несмешивающиеся решеточные газы
  • Вводится отталкивание между частицами разного типа (например, “синими” и “красными”).
  • При достаточной силе отталкивания происходит разделение веществ.
  • Это достигается перераспределением цвета частиц после столкновений так, чтобы красные частицы в основном направлялись в узлы с преобладанием красного цвета и наоборот.
• Модель LGA с переходом “жидкость-газ”
  • Вводится притяжение между частицами, находящимися на некотором расстоянии.
  • Импульсы частиц поворачиваются друг к другу, если это возможно, с учетом закона сохранения импульса согласно третьему закону Ньютона.
  • При достаточно большой длине взаимодействия в некотором диапазоне плотностей возможно сосуществование плотной (жидкой) и разреженной (газообразной) фаз.

Модель LBE с внешними силами и фазовыми переходами

Действие внешних сил

• Моделирование сил, действующих на вещество.
  • Природа сил может быть самой разной (например, электрические силы, сила тяжести, силы межмолекулярного взаимодействия и т.д.).
  • Суммарная сила, действующая на вещество в узле, равна $F$.
  • Действие силы в течение шага по времени $\Delta t$ приводит к изменению скорости: $\Delta u = \frac{F \Delta t}{\rho}$.
  • Решеточное уравнение Больцмана принимает вид: $f_k(x + c_k \Delta t, t + \Delta t) = f_k(x, t) + \Omega_k(x, t) + \Delta f_k$. То есть, после действия оператора столкновений (в котором используется скорость $u$), необходимо учесть изменение функций распределения $\Delta f_k$ под действием сил. Эта добавка равна разнице равновесных функций распределения при одной и той же плотности, но с разными скоростями: $\Delta f_k = f_k^{eq} (\rho, u + \Delta u) - f_k^{eq} (\rho, u)$.
• Порядок учета действия сил:
  1. Вычислить промежуточные значения функций распределения: $f^*_k(x, t + \Delta t) = f_k(x, t) + \Delta f_k$.
  2. Применить оператор столкновений: $f_k(x, t + \Delta t) = f^_k(x, t + \Delta t) + (f^{eq}_k (u + \Delta u) - f^_k(x, t + \Delta t)) / \tau$.
• Физическая скорость вещества:
  • $u^* = \frac{u + (u + \Delta u)}{2} = u + \frac{\Delta u}{2}$.
    • На каждом шаге по времени в каждом узле существуют два значения скорости — до и после действия сил.
    • В случае действия сил физическая скорость вещества равна их среднему арифметическому.

Фазовые переходы

• Достаточно простой способ моделирования фазовых переходов жидкость – пар.

• Между частицами, находящимися в соседних узлах, задается сила взаимодействия:

  $F(x) = \psi(\rho(x)) \sum_k G_k e_k \psi(\rho(x + e_k))$.

  • Значения коэффициентов $G_k > 0$ соответствуют притяжению между соседними узлами, что необходимо для сосуществования жидкой фазы и паровой фазы. В обратном случае при $G_k < 0$ — отталкивание.
  • $G_k$ выбираются таким образом, чтобы сила была достаточно изотропной (чтобы, например, капли получались круглыми).
  • При использовании модели LBE на квадратной сетке сила взаимодействия между узлами, расположенными по диагонали на расстоянии $\sqrt{2}$, должна быть в 4 раза меньше, чем между ближайшими соседями, то есть $G_{1-4} = G_0 > 0$, а $G_{5-8} = \frac{G_0}{4}$.
  • «Эффективная плотность» $\psi(\rho)$ может выбираться достаточно произвольно.
  • Введение такого взаимодействия приводит к уравнению состояния, которое связывает давление, плотность и температуру.

Заключительная часть

Заключение

Методы решеточных газов и решеточного уравнения Больцмана предоставляют мощный инструмент для моделирования сложных физических процессов, включая гидродинамику, теплопередачу и фазовые переходы. Их простота и возможность параллельных вычислений делают их перспективными для изучения широкого класса задач в физике и инженерии. Модели LGA позволяют упростить расчеты и учитывать сложные взаимодействия между частицами, а метод LBE позволяет устранить статистический шум и моделировать макроскопические параметры вещества.

Выводы

Во время выполнения первого этапа группового проекта мы сделали теоретическое описание решеточного уравнения Больцмана и определили задачи дальнейшего исследования.

Список литературы

1. Медведев Д.А. и др. Моделирование физических процессов и явлений на ПК: Учеб. пособие. // Новосибирск: Новосиб. гос. ун-т, 2010. 101 с.

2. Куперштох А. Л. Моделирование течений с границами раздела жидкость-пар методом решеточных уравнениях Больцмана // Вестник НГУ. Сер. Математика, механика и информатика. 2005. Т. 5, № 3. с. 29–42.

3. Chen S., Lee M., Zhao K. H., Doolen G. D. A lattice gas model with temperature // Physica D. 1989. V. 37. p. 42–59.

4. Чащин Г.С. Метод решёточных уравнений Больцмана: моделирование изотермических низкоскоростных течений // Препринты ИПМ им. М.В.Келдыша. 2021. № 99. 31 с..