Видеопрезентация второго этапа группового проекта:

2 Этап проекта Команда 4 Защита на RUTUBE

Постановка проблемы

Моделирование газовых потоков и жидкостей традиционными методами, такими как уравнения Навье-Стокса, требует значительных вычислительных ресурсов.

Методы LGA и LBE предлагают альтернативу, упрощая вычисления при сохранении физической достоверности.

Актуальность

1. Исследования сложных многокомпонентных течений.
2. Течений с фазовыми переходами и химическими реакциями.
3. Создания высокопроизводительных параллельных алгоритмов.

Рассмотрим основные алгоритмы и модели, используемые для решения задач с применением LGA и LBE.

Объект и предмет исследования

• физические процессы в газах и жидкостях
• использование решеточных методов (LGA и LBE) для описания динамики частиц на дискретной сетке

Цель

Исследовать алгоритмы решения задачи с применением LGA и LBE.

Основная часть

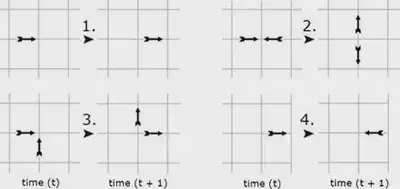
Модель HPP (Hardy–Pomeau–Pazzis). Описание

Модель HPP (Hardy-Pomeau-Pazzis) представляет собой дискретную систему, где пространство и время дискретизованы, а частицы двигаются по узлам квадратной решетки.

Основные характеристики

1. Решетка: Двумерная квадратная
2. Частицы: Единичной массы, 4 направления
3. Скорость: Δx/Δt = 1
4. Принцип исключения: ≤1 частица/направление
5. Эволюция: Распространение → Столкновения
6. Столкновения: Сохранение импульса, 90° поворот
7. Кодирование: 4-битный формат (1 бит/направление)

Основные операции для работы с состояниями узлов

1. Добавление частицы: добавление к состоянию $S$ частицы с направлением скорости $d_k$: $$ S \text{ OR } d_k \rightarrow S $$

2. Проверка наличия частицы: проверка, есть ли в состоянии $S$ частица с направлением скорости $d_k$: $$ \text{if } (S \text{ AND } d_k) \neq 0 $$ Если результат не равен 0, то частица с направлением $d_k$ присутствует в узле.